Quiso la suerte ponerme el desafío de programar un generador de cartones para el juego de bingo. A continuación, voy a explicar la forma en que lo resolví.
A partir de varias consultas que surgieron de este artículo, creamos una demo que contiene algunas funciones de la aplicación.
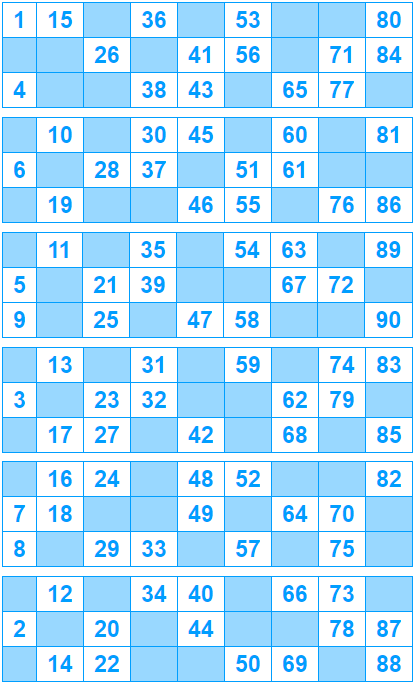
El cartón de bingo está compuesto de una tabla de 3 filas por 9 columnas. En cada fila hay 5 celdas al azar que contienen un número, y 4 que están vacías. Entonces, un cartón contiene en total 15 espacios con números y 12 espacios vacíos.
Una serie corresponde con 6 cartones, que juntos contienen los 90 números que se sortean en el bingo.
Como ya veremos, la distribución de los espacios numerados y vacíos tiene sus reglas, esta es la imagen de una serie:
Ahora bien, para realizar esto debemos dividir el trabajo en 3 partes. La primera, es la construcción de todos los diseños de cartones posibles. La segunda, es combinar esos cartones para obtener la cantidad de diseños de series que queremos. Por último, distribuir aleatoriamente los 90 números en los diseños de series.
Crear los diseños de cartones
Le llamaremos diseño, porque el cartón no tendrá aún sus números. El diseño de un cartón debe cumplir con tres reglas.
La primera regla, después de dos celdas iguales debe haber una opuesta, por ejemplo, si tenemos dos celdas vacías, la siguiente, debe contener un número. Esto vale tanto en el sentido horizontal, como en el vertical.
La segunda regla, no puede haber grupos de 2 por 2 celdas iguales. Como en el caso anterior, la cuarta celda del grupo con estas características debe tener un valor opuesto.
La tercera regla la comentamos al inicio, cada fila debe tener 5 espacios numerados y 4 vacíos. Esto lo logramos generando un análisis temprano de bloques. Un bloque tiene 3 celdas, un bloque A tendrá dos de ellas numeradas y una vacía; un bloque B tendrá una celda numerada y dos vacías. Una imagen puede más que cualquier explicación:
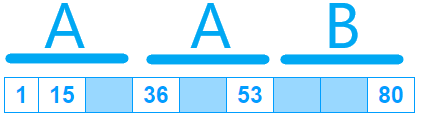
Una fila estará compuesta siempre por dos bloques A y uno B, en cualquiera de las combinaciones posibles.
El algoritmo es una función recursiva que analiza cada celda y comprueba si puede estar vacía y/o puede estar numerada. La solución es que hay 7176 diseños posibles de cartones.
Crear diseños de series
La serie debe tener los números del 1 al 90 ordenados en las columnas según su decena, es decir, en la columna 1, los números del 1 al 9; en la columna 2, los números del 10 al 19; y así hasta la columna 9 que incluirá también el número 90.
Por lo tanto, la serie de 6 cartones debe sumar en la columna 1, 9 celdas numeradas; en las columnas 2 a 8, 10 celdas numeradas; y en la columna 9, 11 celdas numeradas. Esto significa que no todas las combinaciones de 6 diseños de cartones sirven para diseñar una serie.
Combinar los 7176 diseños de cartones para obtener todos los diseños de series posibles es un trabajo poco viable e innecesario, ya que las combinaciones sin repeticiones posibles son 1,892E20, lo cual es un número exageradamente grande.
Lo que hicimos en este caso es salir a “pescar” diseños de series, esto es, tomar al azar un número bajo de cartones, combinarlos y comprobar si cumplen con el requisito para ser una serie. El número de series posibles es elevado, por lo tanto, si queremos variedad, necesitamos limitar en cada “pesca” la cantidad de series que extraemos y realizar una buena cantidad de “pescas”.
Asignar los números
Asignarle los números a un diseño de serie es una tarea relativamente sencilla, la única regla aquí es que, en cada columna de cada cartón, los números se ordenan de menor a mayor. Por ejemplo, en el primer cartón de la serie mostrada al inicio del artículo, la columna 1 tiene los números 1 y 4, deberán estar en ese orden y nunca al revés.
Conclusión
No hemos publicado el algoritmo para realizar esto porque queremos ofrecer la aplicación Bingos que está en nuestra tienda. Por otro lado, es un tema demasiado específico, por lo tanto, si hay algún programador interesado, no tiene más que contactarse con nosotros.